Epithelial tissues play a central role during development of the embryo: they line the surfaces and cavities of organs throughout the body and act as a protective layer, regulating the passage of chemicals to and from underlying tissues, and restricting the invasion of pathogens and harmful substances. We develop and use cell-based models to understand key problems in epithelial morphogenesis, and some key projects are outlined below.

• A. G. Fletcher, F. Cooper and R. E. Baker (2017). Mechanocellular models of epithelial morphogenesis. Philos. Trans. R. Soc. Lond. B Biol. Sci.19(372):1720.  DOI

Vertex-based models for epithelial morphogenesis

We develop and use vertex-based models (VBMs) for epithelial tissues.  These models share the central assumption that a cell may be approximated geometrically by a polyhedron that represents the cell membrane. Within VBMs rules are set up to define how each vertex moves and it is standard to make the following two simplifying approximations: first, that motion relative to a basement membrane may be described by considering each vertex to be embedded in a viscous medium that applies a drag force on it; and second, that inertia is vanishing. This leads to first-order dynamics. The forces applied to vertices are split into two categories: those that manifest as tension forces and represent adhesion at cell-cell junctions; and pressure forces that represent the actomyosin cortex that gives a cell its internal structure. Further rules describe cell rearrangements and control cell birth and death. Repeated simulation of the models generates a series of summary statistics for quantitative comparison with experimental data.

• A. G. Fletcher, M. Osterfield, R. E. Baker and S. Y. Shvartsman (2014). Vertex models of epithelial morphogenesis. Biophys. J. 106(11):2291-2304. DOI
• J. Kursawe, P. A. Brodskiy, J. J. Zartman, R. E. Baker and A. G. Fletcher (2015). Capabilities and limitations of tissue size control through passive mechanical forces. PLoS Comp. Biol. 11(12):e1004679. DOI
• J. Kursawe, R. Bardenet, J. J. Zartman, R. E. Baker and A. G. Fletcher (2016). Robust cell tracking in epithelial tissues through identification of maximum common subgraphs. J. Roy. Soc. Interface. 13(124):20160725. DOI bioRxiv
• J. Kursawe, R. E. Baker and A. G. Fletcher (2017). Impact of implementation choices on quantitative predictions of cell-based computational models. J. Comp. Phys. 345:752-767.  DOI bioRxiv

Rosettes and cell migration

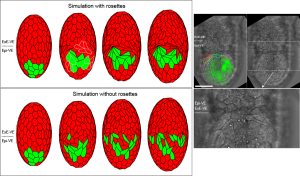
One application of these models by my group was to understand the role of a configuration of cells known as a rosette in facilitating cell migration during early mouse development. Rosettes occur when five or more cells meet at a common vertex, and they were observed by collaborator Dr Shankar Srinivas (University of Oxford) to play a role during migration of a group of cells known as AVE cells. Simulations of a VBM that incorporate rosette formation suggest that while rosettes are not essential for AVE migration, they are crucial for the orderliness of this migration observed in embryos. Our simulations are similar to results from transgenic embryos in which Planar Cell Polarity (PCP) signalling is disrupted. Such embryos have significantly reduced rosette numbers, altered epithelial packing, and show abnormalities in AVE migration. Our results show that the formation of multi-cellular rosettes in the mouse VE is dependent on normal PCP signalling. Taken together, our model and experimental observations suggest that rosettes in the VE epithelium do not form passively in response to AVE migration. Instead, they are a PCP-dependent arrangement of cells that acts to buffer the disequilibrium in cell packing generated in the VE by AVE migration, enabling AVE cells to migrate in an orderly manner.

• G. Trichas, A. M. Smith,  N. White, V. Wilkins,  T. Watanabe, A. Moore, B. Joyce, J. Sugnaseelan, T. A. Rodriguez, D. Kay, R. E. Baker, P. K. Maini and S. Srinivas (2012). Multicellular rosettes in the mouse visceral endoderm facilitate the ordered migration of AVE cells. PLoS Biol. 10(2):e1001256. DOI

Incorporating chemical signalling into vertex-based models

A theoretical aspect of our work has been to design a computational framework within which the effects of chemical signalling factors on evolving epithelial tissues can be studied. The framework incorporates a VBM, in conjunction with a solver for the partial differential equations governing evolution of the chemical concentrations. The VBM provides a natural mesh for the finite element method (FEM), with node movements determined by specified force laws. The arbitrary Lagrangian-Eulerian formulation is adopted to account for domain movement between iterations of the model.

• A. M. Smith, R. E. Baker, D. Kay and P. K. Maini (2012). Incorporating chemical signalling factors into cell-based models of growing epithelial tissues. J. Math. Biol. 65(3):441-463. DOI