Discrete-state, continuous-time Markov models are widely used in the modelling of biochemical reaction networks. Their complexity generally means that they are analytically intractable, and so we rely on simulation-based approaches to estimate system statistics of interest. A large part of my research therefore focusses on developing efficient algorithms for simulating stochastic reaction-diffusion models.

Multi-level Monte Carlo methods

One of the most widely used methods to simulate stochastic models of biochemical reaction networks is the Gillespie algorithm. The Gillespie algorithm generates sample paths one reaction at a time;  it is exact but computationally complex. As such, approximate stochastic simulation algorithms such as the tau-leap algorithm are often used. Here, sample paths are simulated by taking leaps of length tau through time and using an approximate method to generate reactions within leaps. Tau must be held relatively small to avoid significant bias, but this often entails computational times similar to the Gillespie algorithm.

The multi-level method of Anderson and Higham tackles this issue by  generating a suite of sample paths with different accuracies and combining them to estimate system statistics. A base estimator is computed using many (cheap) sample paths at low accuracy. The bias inherent in this estimator is then reduced using a number of correction estimators. Each correction term is estimated using a collection of (expensive) paired sample paths; one path of each pair is generated at a higher accuracy compared to the other. By sharing randomness between these paired sample paths only a relatively small number of them are required to calculate each correction term.

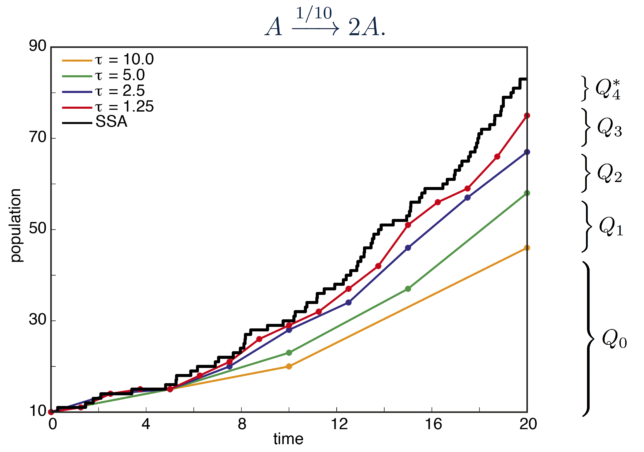
We have made significant extensions to the original multi-level Monte Carlo approach so that it is more broadly applicable to the study of biochemical reaction networks. For example, in the original multi-level method, sample paths are simulated using the tau-leap technique with a fixed value of tau. This approach can result in poor performance where the reaction activity of a system changes substantially over the course of a sample path. We have developed a method that allows for adaptive tau-leaping within the multi-level framework.

• C. H. L. Beentjes and R. E. Baker (2019). Uniformisation techniques for stochastic simulation of chemical reaction networks. J. Chem. Phys. 150(5):154107 DOI arXiv
• C. H. L. Beentjes and R. E. Baker (2018). Quasi-Monte Carlo methods applied to tau-leaping in stochastic biological systems. Bull. Math. Biol. 81(8):2931-2959. DOI arXiv
• C. Lester, C. A. Yates and R. E. Baker (2018). Robustly simulating biochemical reaction kinetics using multi-level Monte Carlo approaches. J. Comp. Phys. 35:1401-1423. DOI arXiv
• C. Lester, C. A. Yates and R. E. Baker (2017). Efficient parameter sensitivity computation for spatially-extended reaction networks. J. Chem. Phys. 146:044106. DOI arXiv
• D. Wilson and R. E. Baker (2016). Multi-level methods and approximating distribution functions. AIP Adv. 6:075020. DOI arXiv
• C. Lester, R. E. Baker, M. B. Giles and C. A. Yates (2016). Extending the multi-level method for the simulation of stochastic biological systems. Bull. Math. Biol. 78(8):1640-1677.  DOI arXiv
• C. Lester, M. B. Giles, C. A. Yates and R. E. Baker (2015). An adaptive multi-level simulation algorithm for stochastic biological systems. J. Chem. Phys. 124:024113. DOI

Efficient simulation of reaction-diffusion systems

My group also explores other means by which one can efficiently simulate paths for lattice-based reaction-diffusion systems. A recent example of our work is the extension of random walk algorithms to include jumps to non-nearest neighbour sites, and we are currently exploring different methods for coarse graining volume exclusion models, and connecting models at different scales.

• N. T. Fadai, R. E. Baker and M. J. Simpson (2019). Accurate and efficient discretisations for stochastic models of cell migration and cell proliferation with crowding. J. Roy. Soc. Interface 16. DOI bioRxiv
• P. R. Taylor, R. E. Baker, M. J. Simpson and C. A. Yates (2016). Coupling volume-excluding compartment-based models of diffusion at different scales: Voronoi and pseudo-compartment approaches. J. Roy. Soc. Interface 13(120). DOI arXiv
• P. R. Taylor, R. E. Baker and C. A. Yates (2015). Deriving appropriate boundary conditions, and accelerating position-jump simulations, of diffusion using non-local jumping. Phys. Biol. 12(1):016006. DOI
• P. R. Taylor, C. A. Yates, M. J. Simpson and R. E. Baker (2015). Reconciling transport models across scales: the role of volume exclusion. Phys. Rev. E Rapid Communication 92:040701(R). DOI arXiv