Model coarse-graining provides a useful means to derive analytically tractable approximations to individual-based models. We have worked on a range of topics in this area, a few of which are outlined below.
Incorporating the effects of cell shape
Continuum diffusion models are often used to represent the collective motion of cell populations. Most previous studies have simply used linear diffusion to represent collective cell spreading, while others found that degenerate nonlinear diffusion provides a better match to experimental cell density profiles. However, there is no guidance available with regard to which approach is more appropriate for representing the spreading of cell populations. Our work provides a link between individual-based and continuum models using a multiscale approach in which we analyze the collective motion of a population of interacting agents in a generalized lattice-based exclusion process. For round agents that occupy a single lattice site, we find that the relevant continuum description of the system is a linear diffusion equation, whereas for elongated rod-shaped agents that occupy L adjacent lattice sites we find that the relevant continuum description is a diffusion equation with a nonlinear diffusion coefficient. The nonlinear diffusivity function is related to the aspect ratio of the agents. Results suggest that when using continuum models to represent cell population spreading, we should take care to account for variations in the cell aspect ratio because different aspect ratios lead to different continuum models.
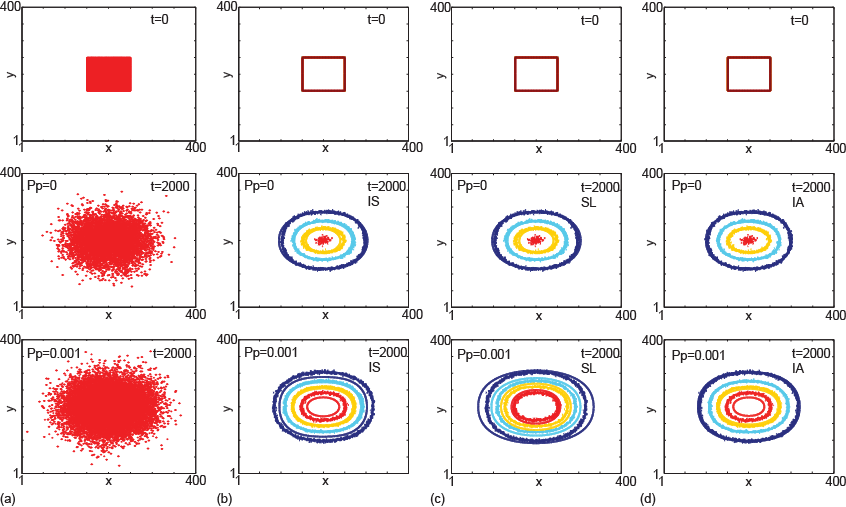
- M. J. Simpson, R. E. Baker and S. W. McCue (2011). Models of collective cell spreading with variable cell aspect ration: a motivation for degenerate diffusion models. Phys. Rev. E. 83(2):021901. DOI
- R. E. Baker and M. J. Simpson (2012). Models of collective cell motion for cell populations with different aspect ratio: diffusion, proliferation and travelling waves. Physica A 391(14):3729-3750. DOI
Coarse-graining off-lattice models
We have also worked towards coarse-grained models for off-lattice volume excluding models to understand how volume exclusion impacts cell motility at a population level.
- L. Dyson, P. K. Maini and R. E. Baker (2012). Macroscopic limits of individual-based models for motile cell populations with volume exclusion. Phys. Rev. E 86(3):031903. DOI
- L. Dyson and R. E. Baker (2014). The importance of volume exclusion in modelling cellular migration. J. Math. Biol. 71(3):691-711. DOI
The role of crowding
Another, closely related, aspect of our work has been to understand the role of crowding upon motility. We have used both computational simulation, and exact methods, to understand how obstacles hinder the motion of randomly moving agents.
- A. J. Ellery, M. J. Simpson, S. W. McCue and R. E. Baker (2014). Characterizing transport through a crowded environment with different obstacle sizes. J. Chem. Phys. 140:054108. DOI
- A. J. Ellery, R. E. Baker and M. J. Simpson (2015). Calculating the Fickian diffusivity for a lattice-based random walk with agents and obstacles of different shapes and sizes. Phys. Biol. 12(6):066010 DOI
- A. J. Ellery, R. E. Baker and M. J. Simpson (2016). Distinguishing between short-time non-Fickian diffusion and long-time Fickian diffusion for a random walk on a crowded lattice. J. Chem. Phys. (Communication) 144(17):171104. DOI
- A. J. Ellery, M. J. Simpson, S. W. McCue and R. E. Baker (2016). Modelling transport through an environment crowded by a mixture of obstacles of different shapes and sizes. Physica A 449:74-84. DOI
- A. J. Ellery, R. E. Baker and M. J. Simpson (2016). An analytical method for disentangling the roles of adhesion and crowding for random walk models on a crowded lattice. Phys. Biol. 13(5):05LT02. DOI
